三相交流

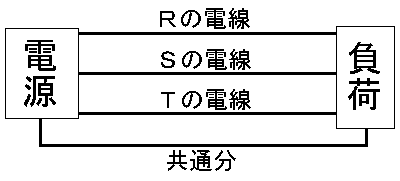
交流モータの次はやっと直流モータの話かと思っていた人がいたら、残念ながら違います。交流モータの最後に“３組の交流を使って”とさらっと書きましたが、そのときの図には３本しか線がありませんでした。模型工作をしたことがある人はわかると思いますが（模型工作をしたことがない人もおそらくわかると思います）、３組の電気を送るには６本の電線が必要になります。その片側を共通にしたとしても共通の１本とあと３本で計４本ないと困りますね。

そうやって交流を３組作って、負荷へ送ってみましょう。３組の交流を区別するため、仮にＲ、ＳとＴという符号をつけてみました。こうすればとりあえず交流を３組送ってモータを回すことができます。この方法は現実に三相４線式といってごく稀に使われています。

ところで、モータをスムーズに回すためには、この３組の交流はどうなっていればいいのでしょうか。まず、３つとも同じ電圧でないとスムーズにいかないでしょう。それから、＋と－になる瞬間が均等にずれていなければなりません。全部揃って同じタイミングで＋になっていたら、モータの中で全部いっせいにＮになってしまい、モータは回りません。大体、同じ電圧で同じタイミングならわざわざ３本の線でつながなくても１本でいいし。

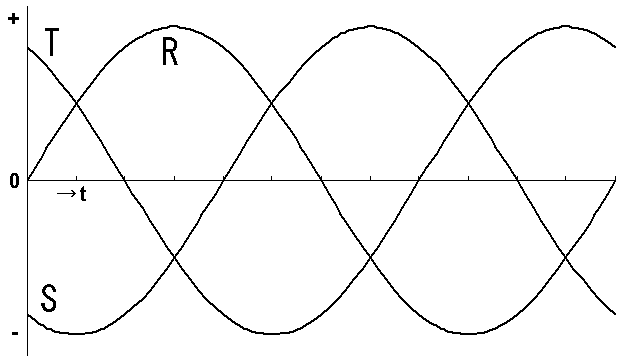
そこで３組の交流を１サイクルの３分の１ずつずらしてみました（左図）。こうすればモータのページで見たように、３つのコイルが順にＮになってモータを回すことができます。電圧を３分の１ずつずらすと、電源も負荷も３組ともまったく同じもの（１台のモータの中身だから）なので、電流も３分の１ずつずれます。力率のページのように電流が遅れたとしても同じ遅れ方をするので、左図は３組の電流の変化と考えてもかまいませんね。では、それぞれの瞬間ごとの電流の合計を考えてみましょう。たとえば、「→ｔ」の文字のすぐ上にある目盛りの瞬間は、ピークが１[Ａ]とするとＲとＴの電流がそれぞれ＋0.5[Ａ]、Ｓの電流が－１[Ａ]ですね。次の目盛りではＴが±０[Ａ]、Ｒが約＋0.866[Ａ]、Ｓが約－0.866[Ａ]、次の目盛りではＲが＋１[Ａ]、ＳとＴが－0.5[Ａ]。・・・てな具合です。さて、このとき共通の線にはどれだけの電流が流れるのでしょう。

キルヒホッフの法則（のページ）を思い出してください。負荷からでている４本の線を流れる電流の合計は０になるはずです。ここから考えると共通の電線を流れる電流をＸ[Ａ]として、「→ｔ」の文字のすぐ上にある目盛りの瞬間は＋0.5＋0.5＋（－１）＋Ｘ＝０、次の目盛りの時は±０＋0.866＋（－0.866）＋Ｘ＝０、その次の目盛りの時は＋１＋（－0.5）＋（－0.5）＋Ｘ＝０。がんばってＸを計算しましょうね。

できましたか、と聞くまでもなく、いずれもＸ＝０となります。３か所の計算をしてみましたが、実はどの瞬間を計算してもＸ＝０が成立します。疑り深い人は、ぜひ任意の瞬間で検算してみてください。

常に合計電流が０ということは、共通の線にはまったく電流が流れないということですね。それなら電線でつないでおく必要はありません。共通の電線そのものをなしにしましょう。これで無事に３本の線で３組の交流を送ることができるようになりましたとさ。めでたしめでたし。